MVP矩阵变换
为什么要进行MVP变换
想在屏幕上呈现一幅画面,首先,我们要把模型变换到世界空间这个模型该在的位置,这就是Model变换,当物体已经在世界空间找到自己的位置的时候,我们就需要把这个世界空间移到摄像机面前,这就是视图变换,最后,因为我们的视角是有一定的角度的,所以并不像正交投影一样看到物体,而是一种透视变换,而这就是投影矩阵,投影矩阵将观察空间的物体投影到成像的屏幕空间,这个时候,我们就可以看到正确的物体,并进行进一步的渲染了,这就是MVP变换。
1.Model矩阵推导
我们只要知道这个物体在世界空间的坐标,就能轻松的得到正确的Model矩阵。
对于最开始的物体坐标
⎣⎢⎢⎢⎢⎢⎢⎢⎢⎡0001⎦⎥⎥⎥⎥⎥⎥⎥⎥⎤→⎣⎢⎢⎢⎢⎢⎢⎢⎢⎡xyz1⎦⎥⎥⎥⎥⎥⎥⎥⎥⎤
只需要平移即可得到,所以Model矩阵为
⎣⎢⎢⎢⎢⎢⎢⎢⎢⎡100001000010xyz1⎦⎥⎥⎥⎥⎥⎥⎥⎥⎤
2.View矩阵推导
我们只需要把摄像机的坐标当成观察空间的零点就可以很轻松的得到视图变换矩阵,需要注意的一点是摄像机的z是与相反的,所以应该是**-z**。设摄像机坐标为 (x,y,z)
所以,View矩阵为
⎣⎢⎢⎢⎢⎢⎢⎢⎢⎡100001000010−x−y−z1⎦⎥⎥⎥⎥⎥⎥⎥⎥⎤
其实这一步默认的摄像机不用旋转角度,如果不默认的话,还需要一步旋转。
3.Projection矩阵推导
我们可以把从观察空间投射到屏幕空间分解成两个部分,一个是将 x, y 大小改变的透视压缩矩阵,另一个是正交投影部分,两个矩阵合成之后,就是所需的投影矩阵。
首先是放缩矩阵的推导:
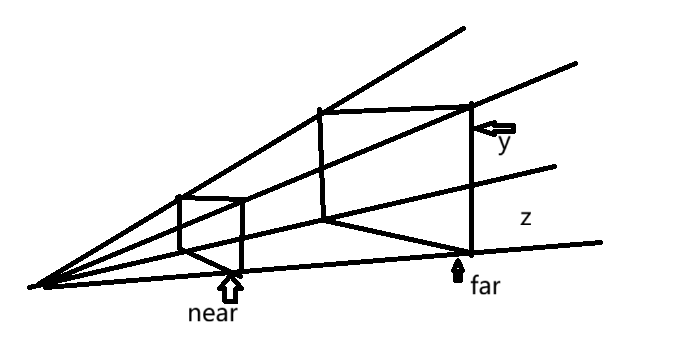
由三角形相似可求,比例为 zn,x→znx,y→zny
我们用 ⎣⎢⎢⎢⎢⎢⎢⎢⎢⎡xyz1⎦⎥⎥⎥⎥⎥⎥⎥⎥⎤ 来表示一个点,那么经过变换之后该点坐标为 ⎣⎢⎢⎢⎢⎢⎢⎢⎢⎡znxzny?1⎦⎥⎥⎥⎥⎥⎥⎥⎥⎤
我们不妨对 x,y 乘一个 f,得到 ⎣⎢⎢⎢⎢⎢⎢⎢⎢⎡nxny?z⎦⎥⎥⎥⎥⎥⎥⎥⎥⎤,那么透视压缩矩阵应为 ⎣⎢⎢⎢⎢⎢⎢⎢⎢⎡n0?00n?000?100?0⎦⎥⎥⎥⎥⎥⎥⎥⎥⎤,现在我们只需要求 ? 的值。
因为变换之后的 z 坐标与 x 和 y 无关,所以前两个 ? 的值都为 0,不妨设后两个 ? 分别为 A,B。
现在只需要求出 A,B 的值,我们可以发现还有两个特性我们并没有用到,那就是近平面和远平面的 z 经过压缩之后并不会改变(这个特性是因为我们想要正交矩阵把 n 和 f 之间的空间压缩到 −1 到 1 之间),所以可以得到两个等式
[00AB]⎣⎢⎢⎢⎢⎢⎢⎢⎢⎡xyn1⎦⎥⎥⎥⎥⎥⎥⎥⎥⎤=n2
,
[00AB]⎣⎢⎢⎢⎢⎢⎢⎢⎢⎡xyf1⎦⎥⎥⎥⎥⎥⎥⎥⎥⎤=f2
解得 A=n+f,B=−nf
所以我们得到了透视压缩矩阵
⎣⎢⎢⎢⎢⎢⎢⎢⎢⎡n0000n0000n+f100−nf0⎦⎥⎥⎥⎥⎥⎥⎥⎥⎤
第二步是正交投影矩阵推导:
目标:把物体中心移动到世界中心,并把物体空间压缩到 [−1,1]3
- 平移矩阵
已知 xn,xf,yn,yf,zn,zf,很容易推导出物体中心坐标为 (2xn+xf,2yn+yf,2zn+zf)
把中心坐标移动到 (0,0,0) 可以推出矩阵为
⎣⎢⎢⎢⎢⎢⎢⎢⎢⎢⎢⎢⎡100001000010−2xn+xf−2yn+yf−2zn+zf1⎦⎥⎥⎥⎥⎥⎥⎥⎥⎥⎥⎥⎤
- 缩放矩阵
我们现在需要把 x,y,z 空间都压缩到 [−1,1]3 这个范围,所以很容易推导出矩阵为
⎣⎢⎢⎢⎢⎢⎢⎢⎢⎢⎢⎢⎢⎢⎡xf−xn20000yf−yn20000zf−zn200001⎦⎥⎥⎥⎥⎥⎥⎥⎥⎥⎥⎥⎥⎥⎤
- 改变z轴方向(可以根据api类型决定是否需要这一步)
需要注意的是,改变z轴方向,由于摄像机一般是左手坐标系,所以我们要改变z轴方向,得到矩阵
⎣⎢⎢⎢⎢⎢⎢⎢⎢⎡1000010000−100001⎦⎥⎥⎥⎥⎥⎥⎥⎥⎤
最后一步:
就是矩阵的合成了,注意矩阵是左乘,所以得到的结果是
⎣⎢⎢⎢⎢⎢⎢⎢⎢⎡1000010000−100001⎦⎥⎥⎥⎥⎥⎥⎥⎥⎤⎣⎢⎢⎢⎢⎢⎢⎢⎢⎢⎢⎢⎢⎢⎡xf−xn20000yf−yn20000zf−zn200001⎦⎥⎥⎥⎥⎥⎥⎥⎥⎥⎥⎥⎥⎥⎤⎣⎢⎢⎢⎢⎢⎢⎢⎢⎢⎢⎢⎡100001000010−2xn+xf−2yn+yf−2zn+zf1⎦⎥⎥⎥⎥⎥⎥⎥⎥⎥⎥⎥⎤⎣⎢⎢⎢⎢⎢⎢⎢⎢⎡n0000n0000n+f100−nf0⎦⎥⎥⎥⎥⎥⎥⎥⎥⎤
得到最终结果为
⎣⎢⎢⎢⎢⎢⎢⎢⎢⎢⎢⎢⎢⎢⎡xf−xn20000yf−yn20000−zf−zn20−xf−xnxn+xf−yf−ynyn+yf−zf−znzn+zf1⎦⎥⎥⎥⎥⎥⎥⎥⎥⎥⎥⎥⎥⎥⎤⎣⎢⎢⎢⎢⎢⎢⎢⎢⎡n0000n0000n+f100−nf0⎦⎥⎥⎥⎥⎥⎥⎥⎥⎤
注意当空间关于x轴和y轴对称时,可以简化。
4.MVP变换
先进行model变换,在进行view变换,最后进行projection变换。
